概括

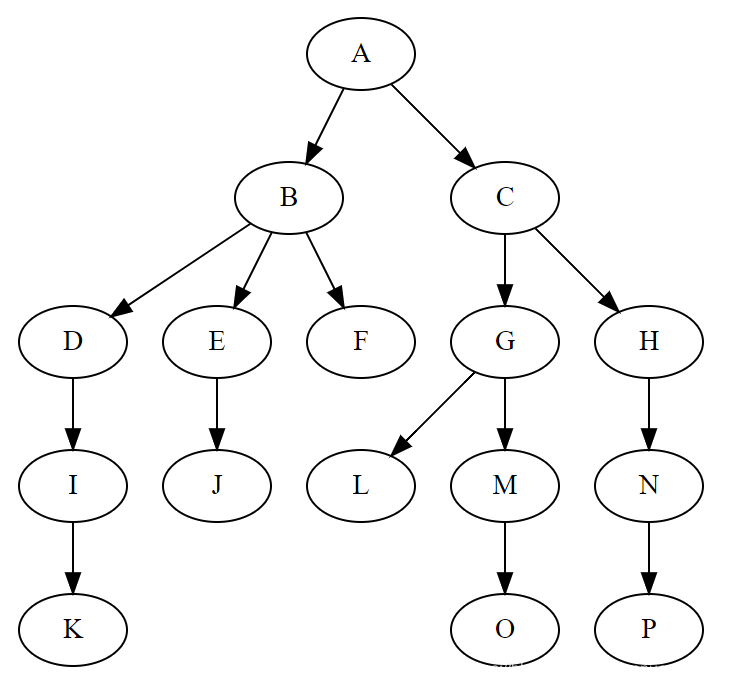
树是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
它具有以下的特点：每个结点有零个或多个子结点；没有父结点的结点称为根结点；每一个非根结点有且只有一个父结点；除了根结点外，每个子结点可以分为多个不相交的子树；
树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。

相关术语

节点的度：一个节点含有的子树的个数称为该节点的度；
叶节点或终端节点：度为0的节点称为叶节点；
非终端节点或分支节点：度不为0的节点；
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
兄弟节点：具有相同父节点的节点互称为兄弟节点；
树的度：一棵树中，最大的节点的度称为树的度；
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；
堂兄弟节点：双亲在同一层的节点互为堂兄弟；
节点的祖先：从根到该节点所经分支上的所有节点；
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
森林：由m（m>=0）棵互不相交的树的集合称为森林；

二叉树

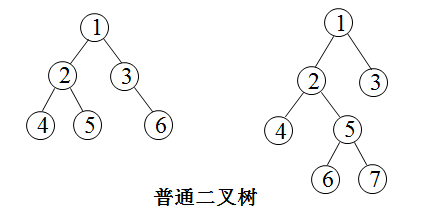
二叉树是数据结构中一种重要的数据结构，也是树表家族最为基础的结构。二叉树每个结点至多拥有两棵子树(即二叉树中不存在度大于2的结点)，并且，二叉树的子树有左右之分，其次序不能任意颠倒。

二叉树遍历

1)先(根)序遍历(根左右)
2)中(根)序遍历(左根右)
3)后(根)序遍历(左右根)

满二叉树

一棵深度为k且有2的k次幂减1个结点的二叉树称为满二叉树。

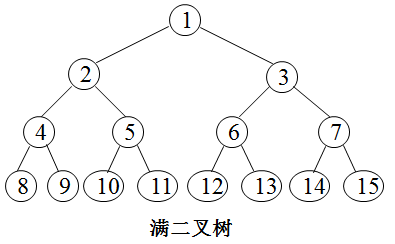
完全二叉树

只有最下面的两层结点度小于2，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。

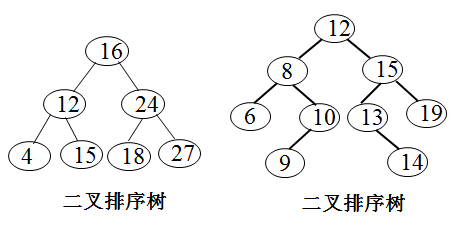
二叉排序树

又称为是二叉查找树（Binary Sort Tree）或二叉搜索树。是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
2. 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
3. 任意节点的左、右子树也分别为二叉查找树；
4. 没有键值相等的节点。
   
   

缺陷

如果key插入类似于随机模型，二叉查找树简洁的实现就能够提供快速的search和insert，以及rank、select、delete和范围查找等。但现实中，worst-case不是不可能发生，例如客户端完全顺序或逆序插入key。这时算法的性能将退化为N，变成线性查找，所以这种可能性也是我们寻找更好算法和数据结构的原因。
二叉查找树的应用不是很多，因为它最坏的时候跟线性表差不多，大部分会应用到它的升级版，平衡二叉树和红黑树，这两棵树都能把时间复杂度稳定在O(logn)左右。虽然不会用到，但是二叉查找树是一定要学好的，毕竟它是平衡二叉树和红黑树的基础。

查找

二叉查找树的查找过程为从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字。

插入

把一个新的记录R插入到二叉查找树，应该保证在插入之后不破坏二叉查找树的结构性质。因此，为了执行插入操作首先应该查找R所在的位置。查找时，仍然采用上述的递归算法。若查找失败，则把包含R的结点插在具有空子树位置，若查找成功，则不执行插入，操作结束。

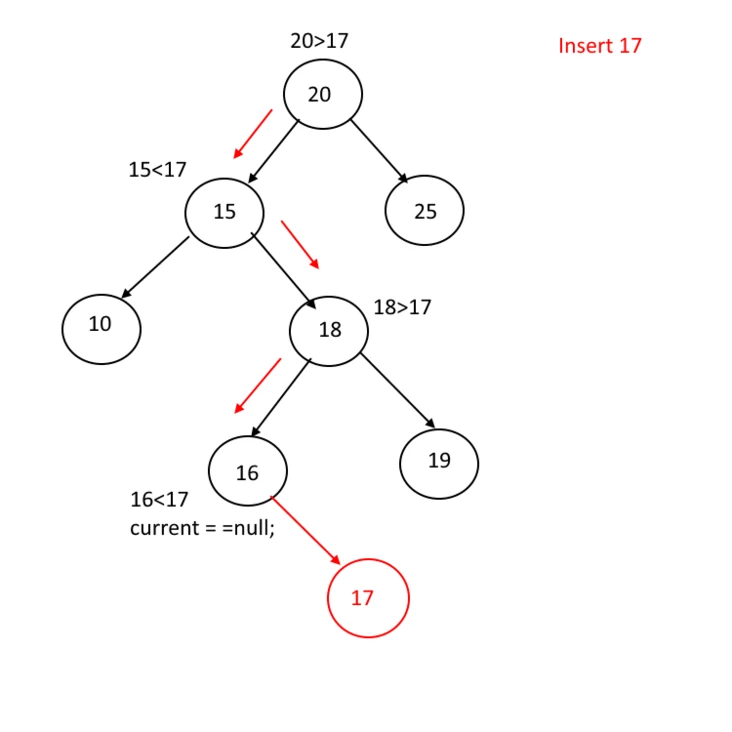
删除

删除叶节点-17

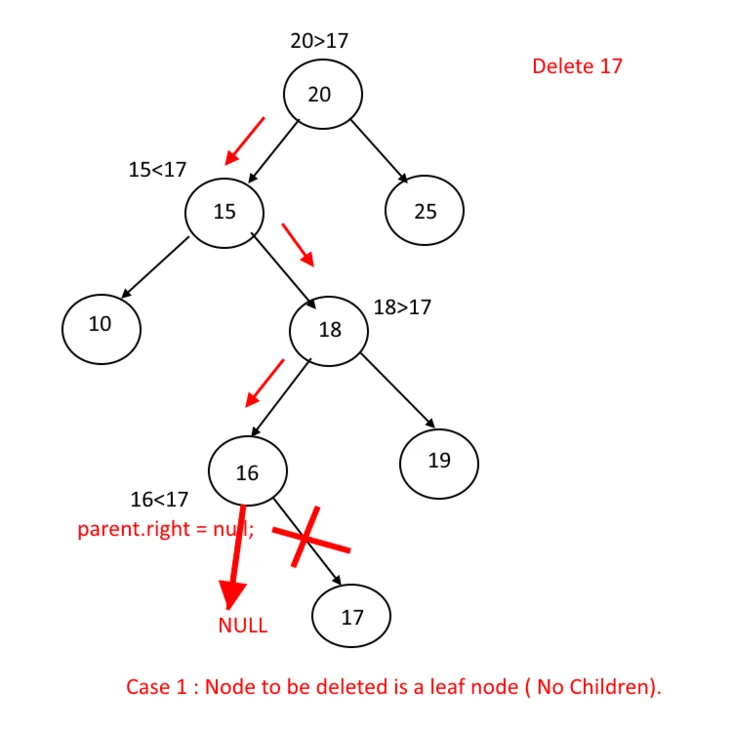
删除只有一个子节点的内部节点-18

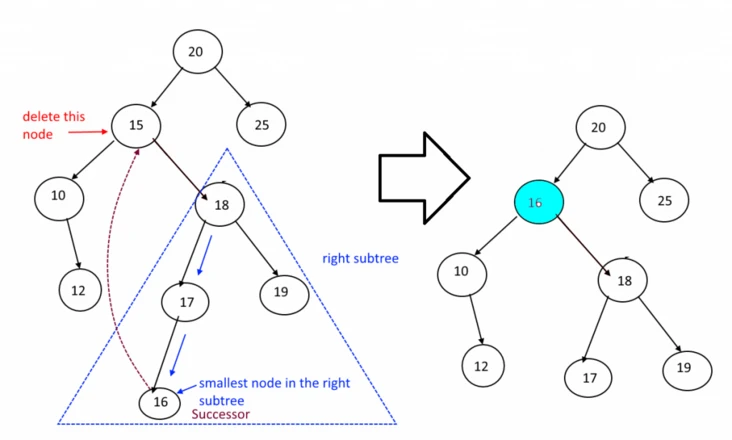
删除有两个子节点的内部节点
如果我们进行简单的替换，那么可能碰到如下情况:

因此我们要在子树中选择一个合适的替换节点，替换节点一般来说会是右子树中的最小的节点: